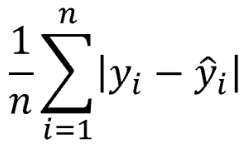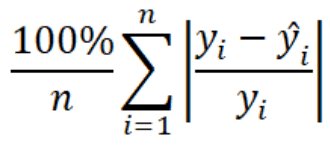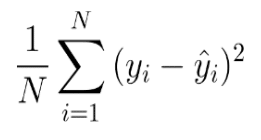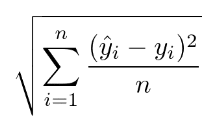En el último artículo de nuestro blog os hablamos ya sobre el potencial de la IA en la predicción de la demanda, recalcando que esta es fundamental en cualquier organización a nivel de planificación y ejecución, no solo por su enorme impacto económico derivado de la disponibilidad de producto, sino también a nivel de eficiencia de las operaciones.
Además, analizamos el rol que la Analítica Avanzada, el ML o la IA juegan en la predicción de demanda y hablamos sobre la importancia del análisis de las series temporales previo a la modelización y los test de validación.
Ahora, en este nuevo post, profundizaremos un poco más acerca de este tema para hablar sobre las métricas de error y las múltiples series temporales, entre otros, y todo esto basándonos en nuestro último webinar: El potencial de la Inteligencia Artificial en la predicción de la demanda. Si te interesa, ¡sigue leyendo!
Métricas de error
Antes de nada, recordarte que para entender mejor todo lo que vamos a hablar, es fundamental que le eches un vistazo a la primera parte de este artículo. Una vez dicho esto, ¡podemos continuar!
Para evaluar la precisión y rendimiento de un modelo (en el dataset de test) se utilizan métricas de error que cuantifican la diferencia entre las predicciones y los valores reales. Entre las más utilizadas se encuentran:
1. MAE (Mean Absolute Error)
Diferencia absoluta media entre las predicciones y los valores reales. Cuanto menor sea el MAE, mejor será el rendimiento del modelo, ya que indica que las predicciones están más cerca de los valores reales en términos absolutos.
Se resta el valor real y el valor predicho para cada punto de datos.
Se toma el valor absoluto de cada diferencia calculada en el paso anterior.
Se calcula el promedio de todas las diferencias absolutas obtenidas.
2. MAPE (Mean Absolute Percentage Error)
Porcentaje medio de error entre las predicciones y los valores reales. Cuanto menor sea el MAPE, mejor será el rendimiento del modelo, ya que indica que las predicciones están más cerca de los valores reales en términos relativos.
Se calcula la diferencia absoluta entre el valor real y el valor predicho para cada punto de datos (paso 1 y 2 del MAE)
Se calcula el porcentaje de cada diferencia absoluta calculada en el paso anterior, es decir, se divide por el valor real y se multiplica por 100.
Se calcula el promedio de todos los porcentajes absolutos obtenidos.
3. MSE (Mean Squared Error)
Media de las diferencias al cuadrado de las predicciones y los valores reales. Cuanto menor sea el MSE, mejor será el rendimiento del modelo.
Se resta el valor real al valor predicho para cada punto de datos.
Se eleva al cuadrado cada diferencia calculada en el paso anterior.
Se calcula el promedio de todos los errores al cuadrado obtenidos.
4. RMSE (Root Mean Squared Error)
Raíz cuadrada del MSE, misma escala que los valores originales.
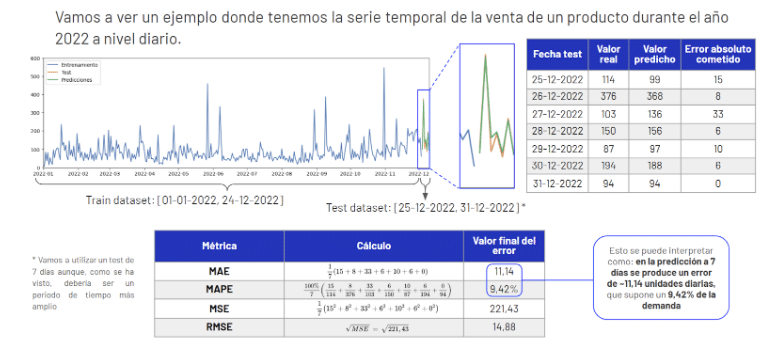
Métricas de error: Ejemplo
Cuándo usar cada una de las métricas
La elección de la métrica de error a utilizar depende de las necesidades del problema específico y de las características de los datos. Cada métrica de error aporta una mirada particular a la medición de la precisión de un modelo.
- El MAE mide el tamaño medio absoluto de los errores sin importar la dirección (positiva o negativa) de ellos. Por otro lado, los valores atípicos (outliers) no se penalizan de manera significativa.
- El MAPE se usa cuando se desea tener una medida relativa del error en porcentaje, lo que permite comparar el error en diferentes escalas, aunque no se puede calcular si hay valores cero en los datos reales. Para solventar ese error, se puede utilizar la variante sMAPE, pero este está acotado entre 0% y 200%.
- El MSE se utiliza cuando se quiere penalizar los errores más grandes, ya que se elevan al cuadrado, aunque es menos interpretable. Si se desea tener esta métrica en la misma escala que los datos originales, se utiliza su raíz cuadrada, el RMSE.
Predicción aislada vs múltiples series temporales
Existen dos posibles estrategias:
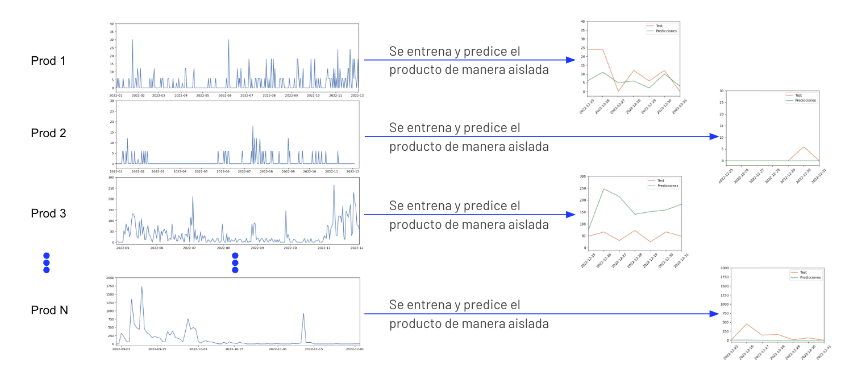
Predicción de una única serie temporal aislada
El modelo se entrena con la información histórica de esa única serie para predecir los siguientes n valores de esa serie.
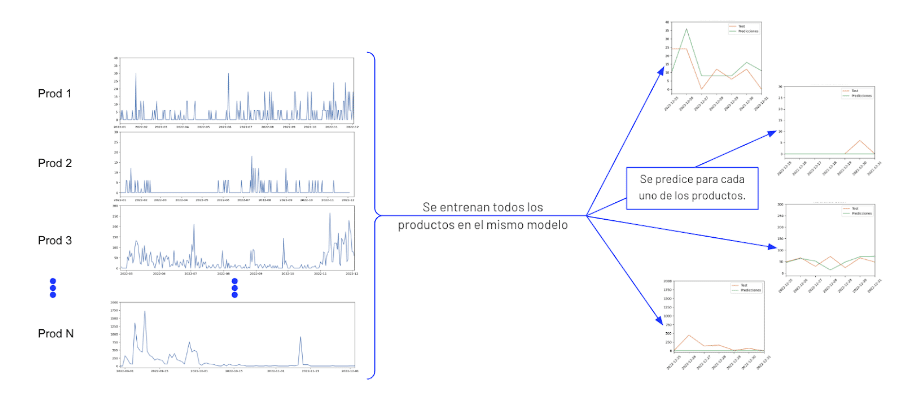
Predicción multi-serie
Varias series temporales se entrenan juntas con un mismo modelo para predecir los siguientes valores para cada una de las series.
La predicción multi-serie puede ser de utilidad al predecir varios productos similares o que se venden en una misma tienda, etc.
Ventajas e inconvenientes de la predicción multi-serie
Ventajas de la predicción multi-serie
- Se tienen en cuenta los valores históricos de todas las series temporales, por lo que el modelo puede aprender ciertas correlaciones entre series
- Por esta razón, el modelo tiene una mayor capacidad de aprendizaje
- También puede generalizar mejor los patrones
Inconvenientes de la predicción multi-serie
- Al combinar varias series temporales, el modelo puede aprender patrones que no representan ninguna serie
- Las series temporales se pueden enmascarar unas a otras haciendo que la precisión de la predicción baje
Inclusión de variables complementarias
Tanto en el caso de predicción de una serie temporal aislada como en el caso de una predicción multi-serie, se pueden incluir variables exógenas en la predicción.
Pueden ser variables referentes al SKU que estamos modelizando, por ejemplo:
- Categoría del producto modelizado
- Precio del producto modelizado
- Promoción del producto
También pueden ser variables totalmente exógenas, de contexto, como por ejemplo:
- Temperatura
- Día de la semana
- Variables económicas
- … etc
Esta información complementaria puede ser de mucha utilidad para que el algoritmo detecte patrones de datos.
Tipos de algoritmos
Existen multitud de algoritmos posibles a aplicar en un proyecto de predicción de demanda. A continuación os mostramos las principales categorías y ejemplos en cada una de ellas.
1. Algoritmos de regresión
Buscan la relación entre la variable dependiente (objetivo) y las variables independientes (predictoras).
Ejemplos:
- Regresión lineal
- Regresión LASSO
2. Algoritmos basados en estadística
Se basan en técnicas y modelos estadísticos para analizar los datos históricos y realizar predicciones.
Ejemplos:
- Suavizados exponenciales
- ARIMA
3. Algoritmos basados en árboles de decisión
Utilizan estructuras de árbol para la toma de decisiones o hacer predicciones. Dividen el conjunto de datos en subconjuntos más pequeños y más homogéneos a medida que se desciende por el árbol.
Ejemplos:
- Random Forest
- Gradient Boosting
- XGBoost
- LightGBM
4. Algoritmos de redes neuronales
Inspirados en el funcionamiento del cerebro humano; utilizan estructuras de redes neuronales artificiales, compuestas por capas de unidades interconectadas para realizar tareas de aprendizaje y predicción.
Ejemplos:
- FNN (Feedforward NNetworks)
- RNN (Recurrent NNetworks)
- LSTM (Long Short-Term Memory)
- GRU (Gated Recurrent Unit)
Combinación de algoritmos
En un proyecto real donde se predice la demanda de uno o varios productos (SKU), en general, no se va a predecir todo a partir de un solo algoritmo, sino que se van a probar varios algoritmos alternativos.
A priori, es difícil determinar qué algoritmo es el mejor para cada serie a modelizar.
Solución: Para cada producto se hace un modelo y se calcula su error en el set de datos de Test (MAE, MAPE o la métrica que se haya escogido)
Se opta por una de estas dos soluciones:
- Solución directa:
Se predice cada producto con su mejor modelo (menor error)
- Solución compuesta:
Ensamble de modelos: Se combinan los modelos de acuerdo a sus errores. Por ejemplo, se pueden ponderar inversamente las predicciones de los modelos por el error que hayan cometido.
En resumen
Los diversos indicadores de error miden la capacidad predictiva de cada modelo aplicado a cualquier serie de datos.
Los datos de input para un modelo predictivo pueden venir de múltiples fuentes. Los propios datos de la serie histórica pueden ser complementados por:
- datos de otras series históricas (productos con características comunes),
- datos de perfil de los productos
- datos de contexto
El uso combinado de distintos modelos puede ser una solución adecuada en entornos de negocio complejos.
Sesión online
¡Y hasta aquí esta segunda parte sobre predicción de demanda! Pero… si os habéis quedado con ganas de más, ya podéis ver en YouTube los 40 minutos de la sesión online donde Joan Miró y Quim Coll explican todos los detalles en relación con los procesos de predicción de demanda.