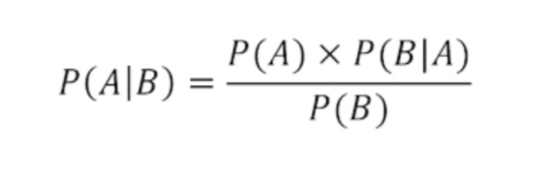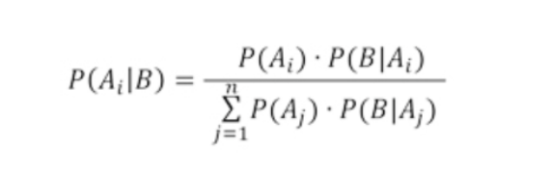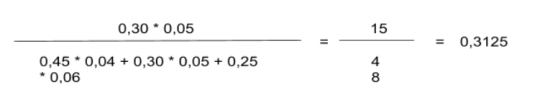El Teorema de Bayes es una proposición matemática ampliamente utilizada en estadística y cálculo de probabilidad. La estadística es uno de los fundamentos del Machine Learning y el Data Science.
La inferencia bayesiana puede beneficiar los análisis de decisión en las empresas, ayudando a encontrar la mejor estrategia basándonos en el cálculo de probabilidades con la información disponible. En Machine Learning se utilizan los algoritmos bayesianos para calcular la probabilidad de que ocurra B si ha ocurrido A, o de saber si ha ocurrido A cuando sabemos que ha ocurrido B, con amplios conjuntos de datos y probabilidades condicionales.
En este artículo trataremos de explicarte de forma sencilla e intuitiva en qué consiste el Teorema de Bayes a través de ejemplos y aplicaciones prácticas.
¿En qué consiste el Teorema de Bayes?
El Teorema de Bayes es una fórmula matemática, diseñada por el matemático británico Thomas Bayes (1702-1761) en el siglo XVIII. Su objetivo es calcular las probabilidades de una hipótesis que se basa en una probabilidad previa o condicional.
Entendemos como probabilidad condicional la posibilidad de obtener una respuesta a una pregunta a partir de los resultados anteriores. Al aplicar la teoría de Bayes, se utiliza la inferencia bayesiana para actualizar la probabilidad de que se cumpla una hipótesis según se obtiene más información.
El Teorema de Bayes tiene multitud de aplicaciones en distintos sectores. En el mundo de la medicina, puede utilizarse para calcular la eficacia de un medicamento teniendo en cuenta el porcentaje de personas con dicha enfermedad que lo conocen y lo toman correctamente. En el ámbito de los Recursos Humanos, puede utilizarse para determinar la probabilidad de que un empleado llegue a ser directivo en función de si cuenta con un MBA o no.
La fórmula del Teorema de Bayes se define de esta forma:
Donde P (A) representa la probabilidad de que ocurra un evento; P (B) la probabilidad de que suceda el evento B; y P (A|B), la probabilidad de que ocurra el evento A en caso de que se haya producido previamente el evento B; y P (B|A), la probabilidad de que ocurra B, en caso de que haya sucedido antes A.
Aplicación del Teorema de Bayes: Ejemplo
Esto se puede explicar más fácilmente con un ejemplo. Supongamos que sabemos que la probabilidad de que haya un accidente en una fábrica que cuenta con alarma es del 0,3%. Y la probabilidad de que la alarma suene cuando se produce un percance es del 0,97% y la probabilidad de que suene la alarma dé un falso positivo es del 0,02%. En el caso de que haya sonado la alarma, ¿qué probabilidades hay de que no haya ocurrido ningún incidente?
El análisis de este ejemplo nos arroja dos posibles sucesos:
A = Se produce un incidente
B = Suena la alarma
Para averiguar las probabilidades de que la alarma suene, pero no haya sucedido ningún incidente, aplicamos la fórmula de Bayes.
P (A|B) = 0,7 * 0,02 / 0,3 * 0,97 + 0,7 * 0,02 = 0,014 / 0,305 = 0,0459
Es decir, la probabilidad de que sonando la alarma, no haya ocurrido ningún incidente, es del 0,0459%. El Teorema de Bayes nos permite además retroalimentar la serie de sucesos con nueva información que vayamos obteniendo. Cuanta mayor sea la información disponible, más preciso podrá ser el cálculo de probabilidades, ya que éstas pueden depender unas de otras.
Veamos un ejemplo con la versión extendida de la fórmula del Teorema de Bayes.
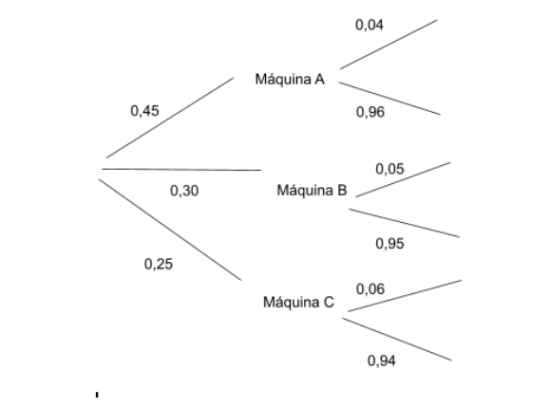
En una fábrica hay 3 máquinas, las cuales producen el 45%, 30% y 25% de todas las piezas producidas en dicha fábrica. Estas máquinas tienen un índice de producción de unidades defectuosas del 4%, 5% y 6% respectivamente. Si seleccionamos una pieza al azar, ¿cuál es la probabilidad de que sea defectuosa?
Para ello, aplicaríamos el teorema de Bayes basándonos en un diagrama de árbol, donde: D = Unidad defectuosa; y N = Unidad no defectuosa
Si queremos averiguar la probabilidad de que sea una unidad defectuosa P (D), lo calculamos de esta forma.
P (D) = P (A) * P (D|A) + P (B) * P (D|B) + P (C ) * P (D|C) = 0,45 * 0,04 + 0,30 * 0,05 + 0,25 * 0,06 = 0,048
En caso de que elijamos al azar una pieza defectuosa, el teorema de Bayes también nos permite averiguar la probabilidad de que pertenezca a la máquina B.
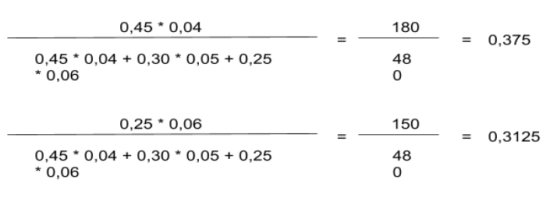
Aquí sería necesario calcular P (A|B):
Donde el resultado sería que la pieza defectuosa tiene un 31,25% de posibilidades de pertenecer a la máquina B.
En último término, también podemos calcular qué máquina tiene mayores probabilidades de haber producido una pieza defectuosa. El procedimiento sería calcular P (A) y P (C), y comparar el resultado con P (B).
Vemos así que la máquina B y la máquina C tienen la misma probabilidad de producir una unidad defectuosa, y que la máquina A es la que más probabilidades tiene de producir unidades defectuosas.
¿Por qué se utiliza el teorema de Bayes en el aprendizaje automático?
Como hemos explicado, el Teorema de Bayes permite averiguar la probabilidad de que ocurra una serie de eventos dado que han sucedido otros anteriormente. Y además, se puede lograr un mayor grado de precisión en el cálculo de probabilidades a medida que introducimos nueva información. ¿Qué tiene esto que ver con el aprendizaje automático?
Algunas de las aplicaciones de Machine Learning se basan en modelos de Naive Bayes, un tipo de algoritmo de clasificación basado en la técnica del Teorema de Bayes. Gracias a los algoritmos basados en el Teorema de Bayes, se pueden llevar a cabo predicciones y análisis de probabilidades precisos que ayuden en la toma de decisiones o la automatización de procesos.
El Data Science permite que se puedan procesar miles y miles de datos, haciendo los cálculos de probabilidades en menos tiempo y de una forma precisa, combinando una gran cantidad de variables combinadas.
Aplicaciones de Machine Learning basadas en la inferencia bayesiana
En Machine Learning se utiliza la inferencia bayesiana para hacer predicciones precisas y aplicables en distintos ámbitos. Te mostramos algunos ejemplos de aplicaciones de algoritmos de inferencia bayesiana que pueden ser de utilidad en las empresas.
Filtrado de correo spam
Un ejemplo de inferencia bayesiana con un modelo Machine Learning es el filtrado de correo spam. El modelo bayesiano tendrá en cuenta las palabras de los mensajes y les asignará un valor según los términos que aparecen en los mensajes de spam o no spam.
A través del aprendizaje supervisado, se puede entrenar a un algoritmo de Machine Learning para calcular la probabilidad de que distintos eventos (la aparición de determinadas palabras) indique que un correo es spam o no, dependiendo de si aparecen también otras palabras y si anteriormente dicho mensaje ha sido categorizado también como spam.
Diagnóstico médico de enfermedades
Otra de las aplicaciones del Teorema de Bayes en proyectos de Machine Learning son los diagnósticos médicos de enfermedades basándose en casos anteriores. Se trata de averiguar la probabilidad de que un paciente tenga una enfermedad, a través de predicciones estadísticas que tienen en cuenta multitud de variables que pueden afectar al resultado.
Utilizando el conocimiento clínico sobre las enfermedades y síntomas, pueden implementarse soluciones basadas en Machine Learning y Big Data para realizar un diagnóstico preciso y la búsqueda de patrones para saber si una persona puede tener o no una determinada afección.
La inferencia bayesiana suele utilizarse en investigación de enfermedades raras, que requieren el análisis de una amplia variedad de datos, cuyos cálculos manuales serían muy complejos de llevar a cabo si no es a través del aprendizaje automático.
Análisis del comportamiento del cliente
Las empresas acumulan datos sobre el comportamiento de los clientes, lo que nos permite comprender mejor su perfil, detectar patrones y predecir su comportamiento futuro, o las probabilidades de que realice una compra si realizamos una determinada acción.
A través del análisis de datos, se pueden calcular por ejemplo las probabilidades de que un cliente compre el producto B en caso de haber comprado el producto A, o las probabilidades de que haga una devolución basándose en su historial previo.
El Machine Learning ayuda a las empresas a tener un conocimiento más preciso de sus clientes, lo que es clave para la toma de decisiones, la mejora de la automatización de procesos y la inteligencia de negocio,
Esperamos que ahora tengas una visión más completa sobre el importante papel que juega la estadística y el Teorema de Bayes en las aplicaciones de Machine Learning y cómo pueden ayudarte a realizar predicciones más precisas. En Kraz, como consultora analítica que somos, estamos encantados de poder ayudarte y por eso, si quieres recibir asesoramiento sobre cómo convertir tus datos en información relevante para tu negocio, no dudes en contactar con nosotros.